近日，我院艾新波教授的理论成果《Adjust Pearson’s r to Measure Nonlinear Monotone Dependence》被NeurIPS’2024接收。NeurIPS是全球最负盛名的人工智能学术会议之一，在谷歌学术发布的全球学术期刊和会议影响力排名中位列第7，H5 index高达337，与ICML、ICLR并称为人工智能机器学习领域难度最大、水平最高、影响力最强的“三大会议”。

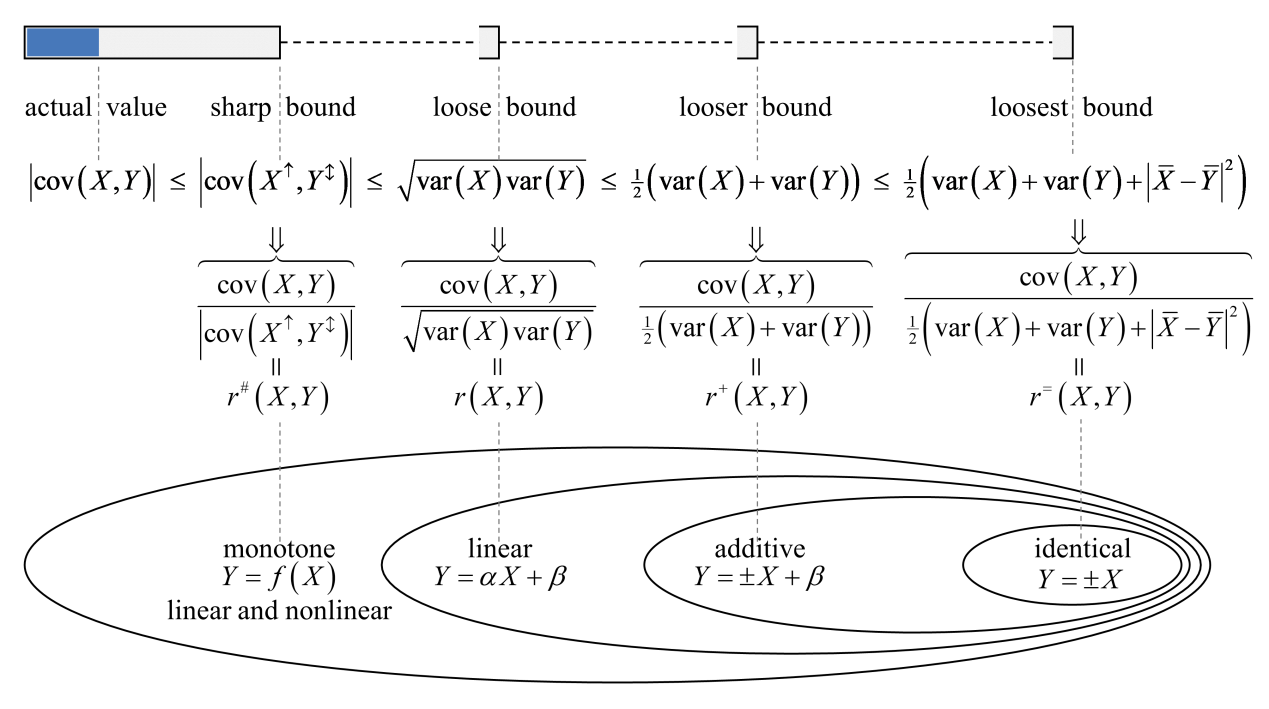
该项成果主要学术贡献是：①为著名的Cauchy-Schwarz不等式找到了一个更加紧致的边界，得到了一个新的不等式系列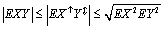；②基于新的不等式，对三大经典相关系数之一的Pearson相关系数进行了改进。改进之后的相关系数，可以度量包括线性关系（linear dependence）在内的任意单调依赖性（monotone dependence）。改进的相关系数，在线性情况下，将退化为Pearson相关系数；在秩上进行计算时，则退化为Spearman相关系数（同样为三大经典相关系数之一）；③该研究表明：现行大部分教材中关于Pearson相关系数的表述，“Pearson相关系数只能用来衡量线性关系”并不准确，更准确的表述可能是“线性关系可以完全被Pearson相关系数所衡量，任意单调依赖性可以在一定程度上被Pearson相关系数衡量”。

论文网址：https://arxiv.org/abs/2205.04571。